AbstractThe algorithm is developed to invert 2D magnetotelluric (MT) data based on sharp boundary parametrization using a Bayesian framework. Within the algorithm, we consider the locations and the resistivity of regions formed by the interfaces are as unknowns.

1. Resistivity Interpretation Software Free Download
2. 3d Resistivity Inversion Software Development Chart
3. 3d Resistivity Inversion Software Development Corporation

Resistivity Interpretation Software Free Download

We use a parallel, adaptive finite-element algorithm to forward simulate frequency-domain MT responses of 2D conductivity structure. Those unknown parameters are spatially correlated and are described by a geostatistical model. The joint posterior probability distribution function is explored by Markov Chain Monte Carlo (MCMC) sampling methods.

The developed stochastic model is effective for estimating the interface locations and resistivity. Most importantly, it provides details uncertainty information on each unknown parameter. Hardware requirements: PC, Supercomputer, Multi-platform, Workstation; Software requirements C and Fortan; Operation Systems/version is Linux/Unix or Windows. Authors: Publication Date: 2010-07-01 Research Org.: Lawrence Berkeley National Laboratory Sponsoring Org.: USDOE OSTI Identifier: 1231818 Report Number(s): STINV-2DMT; 003067MLTPL00 CR-2907 DOE Contract Number: AC02-05CH11231 Resource Type: Software Software Revision: 00 Software Package Number: 003067 Software Package Contents: Media Directory; Software Abstract; Media includes Source Code; / 1 CD-ROM Software CPU: MLTPL Open Source: No Source Code Available: Yes Country of Publication: United States. In this paper, we focus on a hydrogeological inverse problem specifically targeting monitoring soil moisture variations using tomographic ground penetrating radar (GPR) travel time data. Technical challenges exist in the inversion of GPR tomographic data for handling non-uniqueness, nonlinearity and high-dimensionality of unknowns. We have developed a new method for estimating soil moisture fields from crosshole GPR data.

It uses a pilot-point method to provide a low-dimensional representation of the relative dielectric permittivity field of the soil, which is the primary object of inference: the field can be converted to soil moisture using a petrophysical model. We integrate a multi-chain Markov chain Monte Carlo (MCMC)–Bayesian inversion framework with the pilot point concept, a curved-ray GPR travel time model, and a sequential Gaussian simulation algorithm, for estimating the dielectric permittivity at pilot point locations distributed within the tomogram, as well as the corresponding geostatistical parameters (i.e., spatial correlation range). We infer the dielectric permittivity as a probability density function, thus capturing the uncertainty in the inference. The multi-chain MCMC enables addressing high-dimensional inverse problems as required in the inversion setup. The method is scalable in terms of number of chains and processors, and is useful for computationally demanding Bayesian model calibration in scientific and engineering problems. The proposed inversion approach can successfully approximate the posterior density distributions of the pilot points, and capture the true values. The computational efficiency, accuracy, and convergence behaviors of the inversion approach were also systematically evaluated, by comparing the inversion results obtained with different levels of noises in the observations, increased observational data, as well as increased number of pilot points.

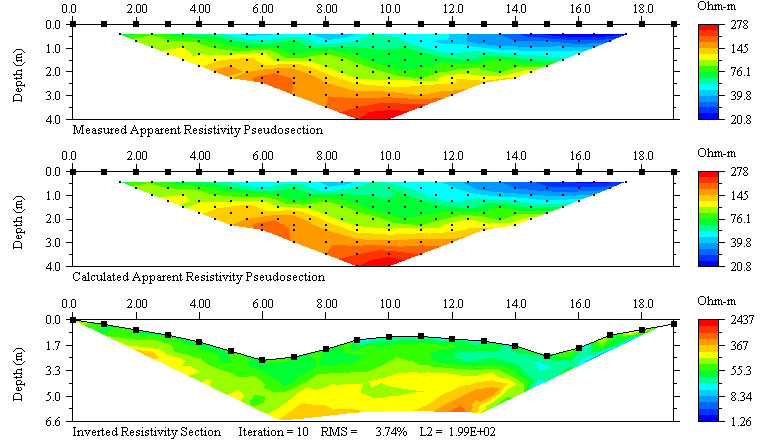
3D inversion of field data collected along 2D profiles, three-dimensional surface grids, boreholes, surface-to-hole arrays, or any 2D or 3D four-electrode array. Sequence generation: a practical toolkit permits easy development of 2D and 3D surface or cross-hole sequences. Survey design: the tetrahedral Finite Element 3D forward modeling module may.

Accidental or terrorist releases of hazardous materials into the atmosphere can impact large populations and cause significant loss of life or property damage. Plume predictions have been shown to be extremely valuable in guiding an effective and timely response. Jay abraham marketing. The two greatest sources of uncertainty in the prediction of the consequences of hazardous atmospheric releases result from poorly characterized source terms and lack of knowledge about the state of the atmosphere as reflected in the available meteorological data. We have developed a new event reconstruction methodology that provides probabilistic source term estimates from field measurement data for both accidental and clandestine releases. Accurate plume dispersion prediction requires the following questions to be answered: What was released?

When was it released? How much material was released? Where was it released? We have developed a dynamic-data-driven event reconstruction capability that couples data and predictive methods through Bayesian inference to obtain a solution to this inverse problem. The solution consists of a probability distribution of unknown source term parameters. For consequence assessment, we then use this probability distribution to construct a 'composite' forward plume prediction that accounts for the uncertainties in the source term. Since in most cases of practical significance it is impossible to find a closed form solution, Bayesian inference is accomplished by utilizing stochastic sampling methods.

This approach takes into consideration both measurement and forward model errors and thus incorporates all the sources of uncertainty in the solution to the inverse problem. Stochastic sampling methods have the additional advantage of being suitable for problems characterized by a non-Gaussian distribution of source term parameters and for cases in which the underlying dynamical system is nonlinear. We initially developed a Markov Chain Monte Carlo (MCMC) stochastic methodology and demonstrated its effectiveness by reconstructing a wide range of release scenarios, using synthetic as well as real-world data. Data for evaluation of our event reconstruction capability were drawn from the short-range Prairie Grass, Copenhagen, and Joint Urban 2003 field experiments and a continental-scale real-world accidental release in Algeciras, Spain.

The method was tested using a variety of forward models, including a Gaussian puff dispersion model INPUFF, the regional-to-continental scale Lagrangian dispersion model LODI (the work-horse real-time operational dispersion model used by the National Atmospheric Release Advisory Center), the empirical urban model UDM, and the building-scale computational fluid dynamics code FEM3MP. The robustness of the Bayesian methodology was demonstrated via the use of subsets of the available concentration data and by introducing error into some of the measurements (Fig.

These tests showed that the Bayesian approach is capable of providing reliable estimates of source characteristics even in cases of limited or significantly corrupted data. An example of an urban release scenario is shown in Fig. For more effective treatment of strongly time-dependent problems, we developed a Sequential Monte Carlo (SMC) approach. To achieve the best performance under a wide range of conditions we combined SMC and MCMC sampling into a hybrid methodology. We compared the effectiveness and advantages of this approach relative to MCMC using a set of synthetic data examples. We created a modular, scalable computational framework to accommodate the full set of stochastic methodologies (e.g., MCMC, SMC, hybrid stochastic algorithms, 'Green's function', 'reciprocal' methods), as well as a selection of key classes of dispersion models.

3d Resistivity Inversion Software Development Chart

This design provides a clear separation of stochastic algorithms from predictive models and supports parallelization at both the stochastic algorithm and individual model level. In other words, it supports a parallel stochastic algorithm (e.g., SMC) that invokes parallel forward models.

The framework is written in Python and utilizes pyMPI. It invokes forward models either through system calls or as shared objects.

Our dynamic-data-driven event reconstruction capability seamlessly integrates observational data streams with predictive models, in order to provide the best possible estimates of unknown source-term parameters, as well as optimal and timely situation analyses consistent with both models and data. This new methodology is shown to be both flexible and robust, adaptable for use with any atmospheric dispersion model, and suitable for use in operational emergency response applications. Although Bayesian analysis has become vital to the quantification of prediction uncertainty in groundwater modeling, its application has been hindered due to the computational cost associated with numerous model executions needed for exploring the posterior probability density function (PPDF) of model parameters. This is particularly the case when the PPDF is estimated using Markov Chain Monte Carlo (MCMC) sampling.

In this study, we develop a new approach that improves computational efficiency of Bayesian inference by constructing a surrogate system based on an adaptive sparse-grid high-order stochastic collocation (aSG-hSC) method. Unlike previous works using first-order hierarchical basis, we utilize a compactly supported higher-order hierar- chical basis to construct the surrogate system, resulting in a significant reduction in the number of computational simulations required. In addition, we use hierarchical surplus as an error indi- cator to determine adaptive sparse grids.

This allows local refinement in the uncertain domain and/or anisotropic detection with respect to the random model parameters, which further improves computational efficiency. Finally, we incorporate a global optimization technique and propose an iterative algorithm for building the surrogate system for the PPDF with multiple significant modes. Once the surrogate system is determined, the PPDF can be evaluated by sampling the surrogate system directly with very little computational cost. The developed method is evaluated first using a simple analytical density function with multiple modes and then using two synthetic groundwater reactive transport models. The groundwater models represent different levels of complexity; the first example involves coupled linear reactions and the second example simulates nonlinear ura- nium surface complexation. The results show that the aSG-hSC is an effective and efficient tool for Bayesian inference in groundwater modeling in comparison with conventional MCMC sim- ulations. The computational efficiency is expected to be more beneficial to more computational expensive groundwater problems.

A Bayesian model selection and parameter estimation algorithm is applied to investigate the influence of nonlinear and unsteady aerodynamic loads on the limit cycle oscillation (LCO) of a pitching airfoil in the transitional Reynolds number regime. At small angles of attack, laminar boundary layer trailing edge separation causes negative aerodynamic damping leading to the LCO. The fluid–structure interaction of the rigid, but elastically mounted, airfoil and nonlinear unsteady aerodynamics is represented by two coupled nonlinear stochastic ordinary differential equations containing uncertain parameters and model approximation errors. Several plausible aerodynamic models with increasing complexity are proposed to describe the aeroelastic system leading to LCO. The likelihood in the posterior parameter probability density function (pdf) is available semi-analytically using the extended Kalman filter for the state estimation of the coupled nonlinear structural and unsteady aerodynamic model.

The posterior parameter pdf is sampled using a parallel and adaptive Markov Chain Monte Carlo (MCMC) algorithm. The posterior probability of each model is estimated using the Chib–Jeliazkov method that directly uses the posterior MCMC samples for evidence (marginal likelihood) computation. The Bayesian algorithm is validated through a numerical study and then applied to model the nonlinear unsteady aerodynamic loads using wind-tunnel test data at various Reynolds numbers.

3d Resistivity Inversion Software Development Corporation

A log of the of the, expressed in ohm-m. The resistivity can take a wide range of values, and, therefore, for convenience is usually presented on a logarithmic scale from, for example, 0.2 to 2000 ohm-m. The resistivity log is fundamental in because hydrocarbons do not conduct electricity while all formation waters do. Therefore a large difference exists between the resistivity of rocks filled with hydrocarbons and those filled with. Minerals and a few other minerals, such as pyrite, also conduct electricity, and reduce the difference.

Some measurement devices, such as and logs, may respond more directly to, but are presented in resistivity.